The given information is:
f(x)=x^2
We need to find the graph of g(x)=f(2x).
We can make a table of values to find the graph of g(x).
As g(x)=f(2x) it means we need to replace the argument x in f(x) by 2x, so:
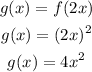
If x=0, so:
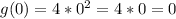
If x=1:
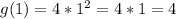
If x=-1:
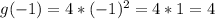
It means the function opens upward, and has its vertex at (0,0).
In the given graph, we can observe the x-axis and y-axis are divided every 2 units, then the first division at the right of the origin is equal to x=2. And the second division over the origin is equal to y=4.
Thus, we can observe in the second graph, that at x=1, the function takes the value y=4, and at x=-1, y=4 too, and the vertex of the graph is located at (0,0).
The answer is then option B.