Question

A rectangular prism can be unfolded into the net shown below. Findthe total surface area of the rectangular prism. Your answer may beexact or rounded to the nearest tenth.4707m108 m676

Answer 1

Consider that the surface area will not be affected by the folding or unfolding of the solid.

So the area of the sheet after unfolding will be equal to the area of the rectangular prism initially.

From the given diagram it is observed that the rectangular prism has length (l), breadth (b), and height (h) as follows,

`\begin{gathered} l=6(7)/(10)=(6(10)+7)/(10)=(67)/(10)=6.7 \\ b=8 \\ h=4(7)/(10)=(4(10)+7)/(10)=(47)/(10)=4.7 \end{gathered}`

Then the surface area of the prism is calculated as,

`\begin{gathered} A=2(lb+bh+lh) \\ A=2*((6.7*8)+(8*4.7)+(6.7*4.7)) \\ A=2*(53.6+37.6+31.49) \\ A=2*122.69 \\ A=245.38 \\ A\approx245.4 \end{gathered}`

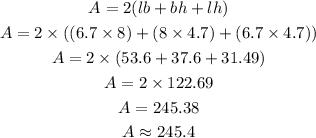
Thus, the area of the rectangular prism is 245.4 sq. meters approximately.