Question

What is the center and radius of the circle indicated by the equation?(x−2)^2+y^2=36

Answer 1

Step-by-step explanation

We are asked to find the centre and radius of the circle equation given as:

`(x-2)^2+y^2=36`

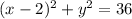
What we will do now will be to compare with the standard equation of a line which is:

`(x-a)^2+(y-b)^2=r^2`

Where

a,b is the centre of the circle

r is the radius of the circle

Thus if we compare the given equation to the standard equation, we will have

`\begin{gathered} (x-2)^2+(y-0)^2=6^2 \\ a=2 \\ b=0 \\ r=6 \end{gathered}`

Thus, the centre is 2,0

the radius is 6