Question

Determine if f(x) = - (x ^ 3)/6 - 6/(x ^ 2) is a polynomial functionIf it is, and the leading coefficient . If not , state why .

Answer 1

Given function is:

`f(x)=-(x^3)/(6)-(6)/(x^2)\ldots(1)`

A polynomial is an algebraic expression that involves only positive integer exponents for the variables.

A polynomial function is of the form:

`p(x)=a_nx^n_{}+a_(n-1)x^(n-1)+a_(n-2)x^(n-2)+\cdots+a_0`

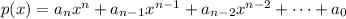
Solving equation (1)

`\begin{gathered} f(x)=-(x^3)/(6)-(6)/(x^2) \\ =-(x^5+36)/(6x^2) \\ =-(x^(-2)(x^5+36))/(6) \end{gathered}`

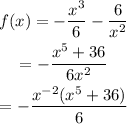
We can see that the function has a negative exponent.

The given function is not a polynomial function.