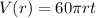Answer::
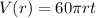
Step-by-step explanation:
For a cone of radius r and height, h
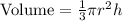
The cone has a fixed height of 15 inches.
The radius increases at a rate of 6 inches per minute.
We have that:
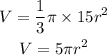
Taking the derivative with respect to time(t), we have:
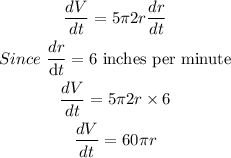
We then rewrite in order to integrate.

Therefore, we have: