Question

IN ONE REGION 40% OF ALL RESIDENTIAL TELEPHONE NUMBERS ARE UNLISTED. IF 5 RESIDENTIAL HOUSING UNITS ARE RANDOMLY SELECTED FIND THE PROBABILITY THAT ALL OF THEM HAVE UNLISTED NUMBERS

Answer 1

Given:

Percentage of numbers unlisted = 40% = 0.40

Sample size, n = 5

Let's find the probability that all 5 of the selected houses have unlisted numbers.

To find the probability, we have:

p(numbers unlisted) = 0.40

Hence, we have:

q = 1 - p = 1 - 0.40 = 0.60

For the probability, apply the binomial probability:

0 .

`P(x=5)=(^5C_5)(0.40)^5(0.60)^(5-5)`

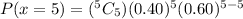
Solving further:

`\begin{gathered} P(x=5)=((5!)/(5!(5-5)!))(0.01024)(0.60)^0 \\ \\ P(x=5)=((5!)/(5!(0)!))(0.01024)(1) \\ \\ p(x=5)=1*0.01024*1 \\ \\ p(x=5)=0.01024 \end{gathered}`

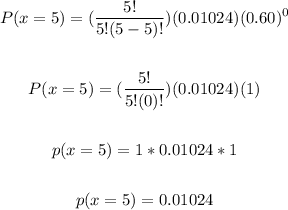
Therefore, the probability that all 5 numbers have unlisted numbers is 0.01024

• ANSWER:

0.01024