Solution:
Given that 836 drank alcohol regularly, 624 smoked cigarettes, 176 used illegal drugs, let

This implies that
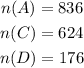
If 395 drank alcohol regularly and smoked cigarettes, 101 drank alcohol regularly and used illegal drugs, 106 smoked cigarettes and used illegal drugs, we have
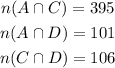
85 engaged in all three behaviors, we have
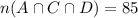
131 engaged in none of these behaviors.
we can represent these data in a venn diagram as follows:
To find how many students were surveyed, we have
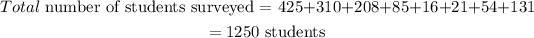
Hence, the total number of students that were surveyed is 1250.