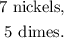To solve this problem, we will set and solve a system of equations.
Let x be the number of nickels you have in your pocket, and y the number of dimes, then with the given information, we can set the following system of equations:
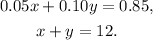
Multiplying the second equation by -0.10 and adding it to the first equation, we get:
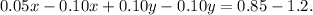
Solving the above equation for x, we get:
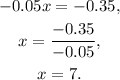
Solving the second equation of the system for y, we get:
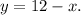
Finally, substituting x=7, we get:
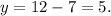
Answer: