Consider that the Reese's peanut butter cup is frustum of cone. So its volume can be obtained by subtracting the voulme of the upper smaller cone from the volume of the full cone.
The volume of a cone with radius of base 'r' and height of cone 'h' is given by,
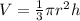
Given that the top has a height 2 cm, and radius 0.8 cm, the corresponding volume is calculated as,
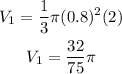
Given that the butter cup has height 1.3 cm, so the height of the complete cone will be the sum of the height of cup and height of smaller cone,
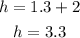
Also the radius of the cup base is 1.3 cm which is also the base of the complete cone. So its volume is given by,
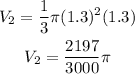
Then the volume of the frustum (V) is calculated as,
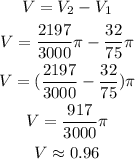
Thus, the volume of the butter cup is approximately 0.96 cubic centimeters.