Answer:
336/527
Step-by-step explanation:
If cos θ = -7/25, then we can represent these angle as:
Because -7 is the adjacent side and 25 is the hypotenuse of the triangle.
So, to know what is tan θ, we need to find the value of x. Then, using the Pythagorean theorem, we get that x is equal to:
![\begin{gathered} x=\sqrt[]{25^2-(7)^2} \\ x=\sqrt[]{625-49} \\ x=\sqrt[]{576} \\ x=24 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/d3mlgax4e50efuna4ifjkw97jch858ih8p.png)
Now, tan θ is equal to:
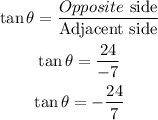
Then, there is a trigonometric identity that says that tan 2θ is equal to:
![undefined]()