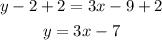Question

Write an equation in slope-intercept form for the line that passesthrough the given point and is parallel to the graph of the given equation.(3,2): y = 3x + 4

Answer 1

You have to find the equation in slope-intercept form for a line that passes through the point (3,2) and is parallel to the line with equation y=3x+4

To determine the equation of the line you need to know the slope of the line and the coordinates of one point. The coordinates of the point are given, to determine the slope you have to use the equation of the parallel line.

If two lines are parallel, then their slope is equal, so the slope of the given line is the same as the slope of the line you have to determine.

The slope of the line with equation y=3x+4 is the coefficient of the x-term, so m=3

Next, use the point-slope form you can determine the equation of the line:

`(y-y_1)=m(x-x_1)_{}`

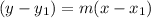
m represents the slope of the line

(x₁,y₁) are the coordinates of one point of the line

Replace the formula using m=3 and (x₁,y₁)=(3,2)

`y-2=3(x-3)`

To write the equation in slope-intercept form, the first step is to distribute the multiplication on the parentheses term:

`\begin{gathered} y-2=3\cdot x-3\cdot3 \\ y-2=3x-9 \end{gathered}`

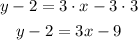
Add 2 to both sides of the equation:

`\begin{gathered} y-2+2=3x-9+2 \\ y=3x-7 \end{gathered}`