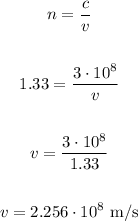Question

5. A light ray travels through the air (n =1.00) at 0 = 35° until it enters a lake(n2=1.33).a. What is the angle of the refracted light?b. Given the index of refraction for the air and the speed of light constant, what is thevelocity of light in air?C. Given the index of refraction for the lake and the speed of light constant, what is thevelocity of the light in the lake?

Answer 1

a.

In order to calculate the angle of the refracted light, we can use the law of refraction below:

`n_1\cdot\sin\theta_1=n_2\cdot\sin\theta_2`

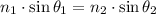
Where n1 and n2 are the index of refraction and theta1 and theta2 are the incident angle and angle of refraction.

So, using n1 = 1, n2 = 1.33 and theta1 = 35°, we have:

`\begin{gathered} 1\cdot\sin\mleft(35°\mright)=1.33\cdot\sin\theta_2\\ \\ 0.5735764=1.33\cdot\sin\theta_2\\ \\ \sin\theta_2=(0.5735764)/(1.33)\\ \\ \sin\theta_2=0.43126\\ \\ \theta_2=25.55° \end{gathered}`

b.

To find the velocity, we can use the formula below:

`\begin{gathered} n=(c)/(v)\\ \\ 1=(3\cdot10^8)/(v)\\ \\ v=3\cdot10^8\text{ m/s} \end{gathered}`

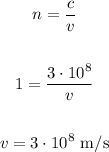
c.

Using the same formula from item b, but now using n2, we have:

`\begin{gathered} n=(c)/(v)\\ \\ 1.33=(3\cdot10^8)/(v)\\ \\ v=(3\cdot10^8)/(1.33)\\ \\ v=2.256\cdot10^8\text{ m/s} \end{gathered}`