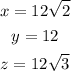Solution:
Given the ΔABC as shown below:
To evaluate the value of x, y, and z,
Let's begin with z.
Step 1: In the ΔBCD, identify the sides.
Thus, in the triangle BCD,
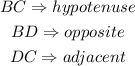
Step 2: Evaluate the value of z, using trigonometric ratios.
From trigonometric ratios,
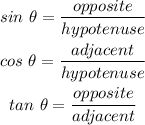
Thus, we have
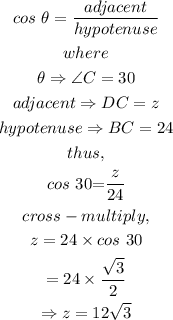
To evaluate the values of x and y, we need to first evaluate the value of BD.
Thus,
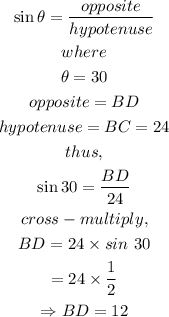
Thus, to evaluate the value of x,
step 1: In the ΔABD, identify the sides of the triangle.
Thus, in the triangle ABD,
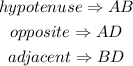
Step 2: Evaluate the value of x, using trigonometric ratios.
From trigonometric ratios,

To evaluate the value of y,
In the triangle ABD, using trigonometric ratios,
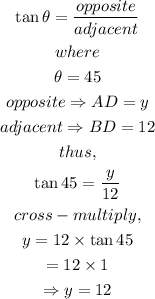
Hence, the values of x, y and z are