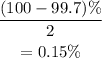Solution:
Given that the normal distribution of data has a mean of 16 and a standard deviation of 2,
we have
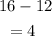
This implies that there are 2 standard deviations.
According to the 68-95-99.7 rule, 99.7% of the population will lie within 3 standard deviations of the mean.
Thus, this means that 99.7% lie between
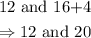
Hence, half of the remainder will be below 12 and the other half will be above 20.
Thus, we have