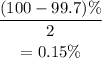Question

Assume that a normal distribution of data has a mean of 16 and a standard deviation of 2 Use the 68-95-99.7 rule to find the percentage of values that lie above 12.What percentage of values lie above 12 ?

Answer 1

Given that the normal distribution of data has a mean of 16 and a standard deviation of 2,

we have

`\begin{gathered} 16-12 \\ =4\text{ } \end{gathered}`

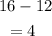
This implies that there are 2 standard deviations.

According to the 68-95-99.7 rule, 99.7% of the population will lie within 3 standard deviations of the mean.

Thus, this means that 99.7% lie between

`\begin{gathered} 12\text{ and \lparen16+4\rparen} \\ \Rightarrow12\text{ and 20} \end{gathered}`

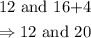
Hence, half of the remainder will be below 12 and the other half will be above 20.

Thus, we have

`\begin{gathered} ((100-99.7)\%)/(2) \\ =0.15\% \end{gathered}`