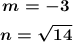Question

Enter the correct answer in the box.Replace the values of m and n to show the solutions of this equation,12 + 6x - 5 = 0

Answer 1

The expression given in the exercise is a quadratic equation in its standard form. To solve any quadratic equation we can use the quadratic formula:

`\begin{gathered} ax^2+bx+c=0\Rightarrow\text{ Quadratic equation} \\ \text{ Where }a\\e0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}\Rightarrow\text{ Quadratic formula} \end{gathered}`

Then, in this case, we have:

`\begin{gathered} x^2+6x-5=0 \\ a=1 \\ b=6 \\ c=-5 \end{gathered}`

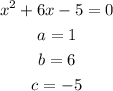
We replace the values of a, b and c in the quadratic formula:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-6\pm\sqrt[]{(6)^2-4(1)(-5)}}{2(1)} \\ \text{ Apply the multiplication sign rule}\colon-\cdot-=+ \\ x=\frac{-6\pm\sqrt[]{6\cdot6+4(1)(5)}}{2} \\ x=\frac{-6\pm\sqrt[]{36+20}}{2} \\ x=\frac{-6\pm\sqrt[]{56}}{2} \\ x=\frac{-6\pm\sqrt[]{4\cdot14}}{2} \\ \text{ Apply the product rule for radicarls property : }\sqrt[n]{ab}=\sqrt[n]{a}\cdot\sqrt[n]{b} \\ x=\frac{-6\pm\sqrt[]{4}\cdot\sqrt[]{14}}{2} \\ x=\frac{-6\pm2\sqrt[]{14}}{2} \\ x=(-6)/(2)\pm\frac{2\sqrt[]{14}}{2} \\ \text{ Simplify} \\ x=-3\pm\sqrt[]{14} \end{gathered}`

Now, since we have the plus and minus symbol in the above expression, then there are two solutions for the given equation:

• First solution

`x_1=-3+\sqrt[]{14}`

• Second solution

`x_2=-3-\sqrt[]{14}`

Therefore, the values of m and n of the solutions of the equation are:

`\begin{gathered} \boldsymbol{m=-3} \\ \boldsymbol{n=√(14)} \end{gathered}`