Question

If you deposit $100 each month into an IRA earning 2.3% interest, how much will you have in the account after 17 years? Round your answer to the nearest cent.

Answer 1

Given:

The amount deposited each month, d=$100.

The rate of interest, R=2.3%.

The number of years after which the balance in the account is calculated, N=17.

The formula for the balance in the acoount after N years is,

`P_N=(d((1+(r)/(k))^(Nk)-1))/(((r)/(k)))\text{ ---(1)}`

Here, r is the interest rate in decimal form and k is the number of compounding periods in one year.

Since deposit is made every month, we use monthly compounding, k=12.

The rate of interest in decimal form is,

`r=(R)/(100)=(2.3)/(100)=0.023`

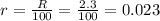
Now, substitute the known values in equation (1).

`\begin{gathered} P_(17)=(100((1+(0.023)/(12))^(17*12)-1))/(((0.023)/(12)))\text{ } \\ P_(17)=(100((1+(0.023)/(12))^(204)-1))/(((0.023)/(12)))\text{ } \\ P_(17)=24934.19 \end{gathered}`

Therefore, after 17 years, the balance in the account will be $24934.19, to the nearest cent.