Question

For a body falling freely from rest ( disregarding air resistance) the distance the body falls varies directly as the square of the time. If an object is dropped from the top of a tower 576 ft high and hits the ground in 6 sec. How far did it fall in the first 4 sec?

Answer 1

In order to solve the question first, we need to identify the structure of the equation, if the distance varies directly to the square of the time it means that the equation will have a constant and look similar to:

`d=k\cdot t^2`

To find the value of K we use the given information saying that the object after 6 seconds hit the ground from a 576 ft tower, then,

`576=k\cdot(6)^2`

solve the equation for k,

`\begin{gathered} k=(576)/(6^2) \\ k=(576)/(36) \\ k=16 \end{gathered}`

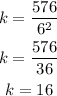
reconstruct the equation,

`d=16t^2`

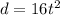
find the distance after 4 seconds using the equation,

`\begin{gathered} d=16\cdot4^2 \\ d=16\cdot16 \\ d=256 \end{gathered}`

Answer:

The object fell 256 ft in the first 4 seconds