Two lines are perpendicular when the multiplication of their slopes is equal to -1.
To find the slope of the line 2x - 3y = 4, we have to isolate y, as follows:
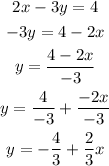
Its slope is 2/3, then the slope of the perpendicular line is:
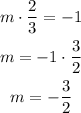
The slope-intercept form is:
y = mx + b
where m is the slope and b is the y-intercept.
Replacing with m = -3/2 and point (3,1):
1 = -3/2(3) + b
1 = -9/2 + b
1 + 9/2 = b
11/2 = b
The equation of the line is y = -3/2x + 11/2