Question

The figure below can be used to prove the Pythagorean Theorem. Use the drop-down menus to complete the proof.

Answer 1

1. 2ab + c^2

2. (a + b)^2 or (a^2 + 2ab + b^2)

3. 2ab

EXPLANATION :

Recall that the area of a triangle is 1/2 base x height.

and the area of a square is the square of its side.

From the problem, we have 4 congruent triangles.

The area of four triangles is :

`\begin{gathered} A=4*(1)/(2)(ab) \\ A=2ab \end{gathered}`

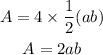
The area of the square is :

`A=c^2`

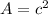
Then the total area will be :

`2ab+c^2`

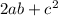
It is equivalent to the area of the whole square in which the side is (a + b)

So that's :

`A=(a+b)^2\quad or\quad(a^2+2ab+b^2)`

Since both expressions are equal, we can equate them :

`\begin{gathered} 2ab+c^2=a^2+2ab+b^2 \\ \text{ Subtracting 2ab from both sides :} \\ 2ab+c^2-2ab=a^2+2ab+b^2-2ab \\ c^2=a^2+b^2 \end{gathered}`