In order to determine the value of f(x) as x approaches to oo, replace larger values of x into the function and identify the tendency of f(x), as follow:
x = 1000
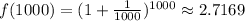
x = 1000000
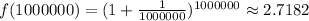
x=1000000000
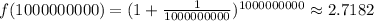
As you can notice, as x approaches to oo, f(x) approaches to 2.7182..., which is the value of constant e.
answer: e