Question

F(x) = 3x2 + 6x – 14g(x) = -2x + 12Find: (gºf)(x)

Answer 1

We are asked to find te composition of function g with f. (gof)(x)

and we are given the following expressions:

`\begin{gathered} f(x)=3x^2+6x-14 \\ g(x)=-2x+12 \end{gathered}`

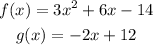
So, we cecall that the composition of functions means that we need to use for the input of the one function (g), the other function (f):

(gof)(x) = g (f(x))

So we proceed to do such

`\begin{gathered} g(f(x))=g(3x^2+6x-14)=-2(3x^2+6x-14)+12= \\ -6x^2-12x+28+12=-6x^2-12x+40 \end{gathered}`

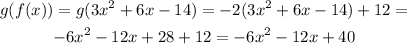
Therefore the composition gives: -6 x^2 - 12 x + 40