Question

Students were asked to simplify the expression the quantity secant theta minus cosine theta end quantity over secant period Two students' work is given.

Answer 1

Trigonometric Identities

Given the expression:

`(\sec \theta-\cos \theta)/(\sec \theta)`

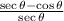
Student A decided to separate the expression into two fractions;

`(\sec \theta)/(\sec \theta)-(\cos \theta)/(\sec \theta)`

Simplified the first term and substituted the secant for its equivalent as the reciprocal of the cosine:

`1-(\cos \theta)/((1)/(\cos \theta))`

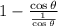
Then simplified the division to get:

`1-\cos ^2\theta`

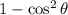
Finally, used the fundamental identity to get:

`\sin ^2\theta`

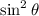
Student A did great.

Student B decided to work on the numerator, substituting the secant by the reciprocal of the cosine as follows:

`((1)/(\cos\theta)-\cos \theta)/(sec\theta)`

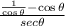
Operated in the numerator:

`((1-\cos ^2\theta)/(\cos \theta))/(sec\theta)`

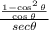
Used the fundamental identity to get the square of the sine, but here he did a mistake. Multiplied cosine by secant and got cosine squared, which is incorrect. He should write the product and then operate;

`(\sin ^2\theta)/(\cos \theta\sec \theta)`

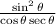
The cosine and the secant are reciprocals of each other, so their product is 1, the denominator vanishes:

`\text{sin}^2\theta`

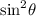
This way, he should have gotten the same result as student A