The volume of a cone is given by
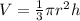
where r is the radius and h is the height of our cone. Since we want the radius, we need to isolate r in this formula. Then, by moving 3 to the left hand side, we have
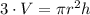
now, by movinf Pi and h to the left hand side, we have
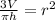
and finally, r is given by
![r\questeq\sqrt[]{(3V)/(\pi h)}](https://img.qammunity.org/2023/formulas/mathematics/college/kqeds78z3e0p32mmvlu2uklnxuw9xqdtqc.png)
Now, we can substitute the given values, V=243Pie, h= 9 and get
![r=\sqrt[]{(3(243\pi))/(\pi(9))}](https://img.qammunity.org/2023/formulas/mathematics/college/se5p1jt1e8cp1d4euq55sdrvasdlzckkcy.png)
We can note that we can cancel out Pie because this number is on the numerator and denominator, then we have
![r=\sqrt[]{(3(243))/(9)}](https://img.qammunity.org/2023/formulas/mathematics/college/e9kl8x74doqb6iuh3qlbtsucq0slw469m4.png)
which gives
![\begin{gathered} r=\sqrt[]{81} \\ r=9 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/r77igni42ylxliozyeh3pz6sspfp6zfn3m.png)
therefore, the radius measure 9 feet.