Question

Why must the first and last term of a perfect square trinomial be both positive?

Answer 1

Given:

The objective is to provide the reason for first and last term of a perfect square trinomial be both positive

Step-by-step explanation:

Consider the following equations,

`\begin{gathered} (a+b)^2=(+a)^2+2(a)(b)+(+b)^2\text{ . . . . . . . (1)} \\ (a-b)^2=(+a)^2+2(a)(b)+(-b)^2\text{ . . . . . . . (2)} \\ (-a+b)^2=(-a)^2+2(a)(b)+(+b)^2\text{ . . . . . . . (3)} \end{gathered}`

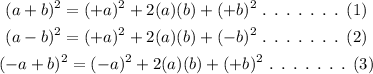
From equations (1), (2) and (3), the first and last term are always perfect squares. So, even when those numbers are negative integer, square of the number will get converted into poitive integer.

Hence, the first and the last term of a perfect square trinomial must be positive.