Question

Which binomial is a factor of the polynomial? x^2 + x - 6

A)(x + 6)
B)(x - 2)
C)(x + 2)
D)(x - 6)

Answer 1

`x^2+x-6`

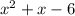
To find the binomial factors, we just need to factorize the expression

To factorise the expression, you look for two factors of 6 that there sum or difference will give the cosfficient of the middle term.

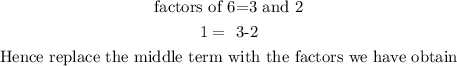
`\begin{gathered} \text{factors of 6=3 and 2} \\ 1=\text{ 3-2} \\ \text{Hence replace the middle term with the factors we have obtain} \end{gathered}`

We have

`x^2+3x-2x-6`

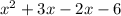
We now take the common factor by splitting the expression into two

`\begin{gathered} x(x+3)-2(x+3)_{} \\ (x-2)(x+3) \end{gathered}`

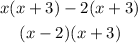
(x-2) is the factor of the polynomial

The r option is B