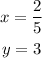Given:
A matrix
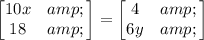
Required:
To find the values of x and y.
Step-by-step explanation:
Two matrices are said to be equivalent matrices if they have the same rank.
The given matrices are equivalent, so their corresponding element will be equal.
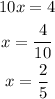
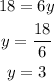
Final Answer:
The values of x and y are as: