Question

Lucia paints a certain room in 5 hours, and Marie paints the same room in 8 hours. How long does it take them to paint the room if they work together? Round to the nearest tenth. _(blank)_ hoursType your numerical answer below.

Answer 1

We need to find the time, t, that it takes them to paint the room working together.

In order to do so, notice that rate at which each of them paint the room, assuming it has an area A to be painted, is:

`\begin{gathered} \text{ Lucia: }(A)/(5h) \\ \\ \text{Marie: }(A)/(8h) \end{gathered}`

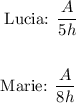
Now, when they work together, Lucia will paint an area A₁, and Marie will paint an area A₂, such that

`A_1+A_2=A`

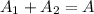
Also, notice that the area each one paints is given by the rate at which they paint multiplied by the time t they spend painting. So, we have:

`\begin{gathered} A_1=(A)/(5h)\cdot t \\ \\ A_2=(A)/(8h)\cdot t \end{gathered}`

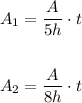
Then, using those expressions for A₁ and A₂ in the equation relating their sum to A, we obtain:

`\begin{gathered} (A)/(5h)\cdot t+(A)/(8h)\cdot t=A \\ \\ (t)/(5h)+(t)/(8h)=1\text{ (dividing both sides by A)} \\ \\ (8t)/(40h)+(5t)/(40h)=1 \\ \\ (13t)/(40h)=1 \\ \\ 13t=1\cdot40h \\ \\ 13t=40h \\ \\ t=(40h)/(13) \\ \\ t\cong3.1h \end{gathered}`

Therefore, rounded to the nearest tenth, it takes them to paint the room working together

3.1 hours