The given linear function is
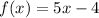
This equation represents a straight line with a slope of 5. (Remember that the slope is the coefficient of the x).
Since we have to find a perpendicular line to f(x), we have to use the perpendicularity criteria to find the slope first:

Where the first slope is 5.
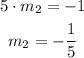
This means the new perpendicular line has a slope of -1/5.
Now, we use this slope, a random point (-1,2), and the point-slope formula, to find the equation

Therefore, a perpendicular line to f(x) would be
