Answer:
The image below will be used to explain the question
From the image above,
We will have the following relationships
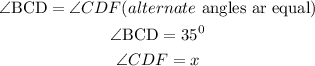
With the relation above, we can conclude that
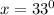
Hence,
The value of x = 33°
Step 2:
The following relation below will be used to calculate the value of y
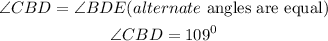
By applying this, we will conclude that
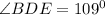
The relation below will be helpful to get the exact value of y
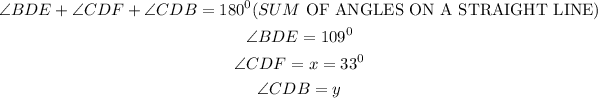
By substituting the values, we will have
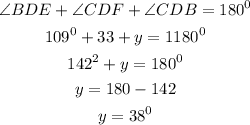
Hence,
The value of y= 38°
The relation below will be used to figure out the value of z
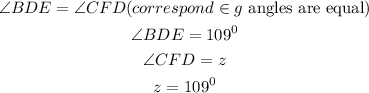
Hence,
the value of z= 109°