Question

Describe the transformation to get from f(x) to g(x) Pls help this is driving me crazy.

g(x)=f(x)-4


g(x)=f(x+6)


g(x)=(1)/(2)f(-x)


g(x)=-f(5x)


g(x)=3f(x+4)-6


g(x)=-f((3)/(2)x)-5

Answer 1

10. A translation of 4 units down.

11. A translation of 6 units left.

12. A reflection in the y-axis, followed by a vertical compression by a factor of ¹/₂.

13. A horizontal compression by a factor of ¹/₅, followed by a reflection in the x-axis.

14. A translation of 4 units left, followed by a vertical stretch by a factor of 3, followed by a translation of 6 units down.

15. A horizontal compression by a factor of ²/₃, followed by a reflection in the x-axis, followed by a translation of 5 units down.

Explanation:

Transformations

`\textsf{For $a > 0$}:`

`f(x+a) \implies f(x) \: \textsf{translated $a$ units left}.`

`f(x-a) \implies f(x) \: \textsf{translated $a$ units right}.`

`f(x)+a \implies f(x) \: \textsf{translated $a$ units up}.`

`f(x)-a \implies f(x) \: \textsf{translated $a$ units down}.`

`a\:f(x) \implies f(x) \: \textsf{stretched parallel to the $y$-axis (vertically) by a factor of $a$}.`

`f(ax) \implies f(x) \: \textsf{stretched parallel to the $x$-axis (horizontally) by a factor of $(1)/(a)$}.`

`-f(x) \implies f(x) \: \textsf{reflected in the $x$-axis}.`

`f(-x) \implies f(x) \: \textsf{reflected in the $y$-axis}.`

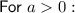
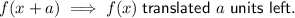
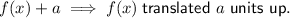
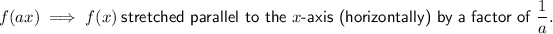
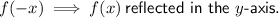
Question 10

`\textsf{Given}: \quad g(x)=f(x)-4`

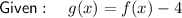
Therefore, the transformation to get from f(x) to g(x) is:

• Translation of 4 units down.

Question 11

`\textsf{Given}: \quad g(x)=f(x+6)`

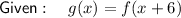
Therefore, the transformation to get from f(x) to g(x) is:

• Translation of 6 units left.

Question 12

`\textsf{Given}: \quad g(x)=(1)/(2)f(-x)`

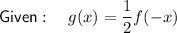
Therefore, the series of transformations to get from f(x) to g(x) is:

• Reflection in the y-axis.
• Vertical compression by a factor of ¹/₂.

Question 13

`\textsf{Given}: \quad g(x)=-f(5x)`

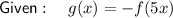
Therefore, the series of transformations to get from f(x) to g(x) is:

• Horizontal compression by a factor of ¹/₅.
• Reflection in the x-axis.

Question 14

`\textsf{Given}: \quad g(x)=3f(x+4)-6`

Therefore, the series of transformations to get from f(x) to g(x) is:

• Translation of 4 units left.
• Vertical stretch by a factor of 3.
• Translation of 6 units down.

Question 15

`\textsf{Given}: \quad g(x)=-f\left((3)/(2)x\right)-5`

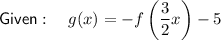
Therefore, the series of transformations to get from f(x) to g(x) is:

• Horizontal compression by a factor of ²/₃.
• Reflection in the x-axis.
• Translation of 5 units down.