Question

There are 24 parents and 8 teachers at a PTO meeting.They are breaking into discussion groups that have 6parents and 2 teachers. How many different groupscan be made?

Answer 1

4 groups!

8 teachers into groups of 2:
2,4,6,8 = 4 groups
6 parents into 2 groups, there are 24 parents:
So 6•4=24

Answer 2

3,768,688 different ways

Step-by-step explanation:

The number of ways to select x elements from a group of n elements is calculated as

`\text{nCx}=(n!)/(x!(n-x)!)`

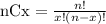
In this case, we want to select 6 parents from a group of 24 and select 2 teachers from the 8 teachers, so

`\begin{gathered} 24C6=(24!)/(6!(24-6)!)=134596 \\ 8C2=(8!)/(2!(8-2)!)=28 \end{gathered}`

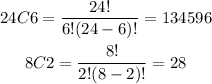
Therefore, the groups can be made in 3,768,688 different ways because

24C6 x 8C2 = 134,596 x 28 = 3,768,688