Question

One number exceeds another by 5.The sum of their squares is 157. What are the numbers?

Answer 1

We have two numbers that we will call x and y.

One number exceeds the other by 5, so we can express it as an equation like:

`y=x+5`

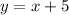
where y exceeds x by 5.

The sum of the squares is 157, so we can express this as:

`x^2+y^2=157`

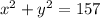
We can replace y with the first expression and obtain:

`\begin{gathered} x^2+(x+5)^2=157 \\ x^2+x^2+10x+25=157 \\ 2x^2+10x+25-157=0 \\ 2x^2+10x-132=0 \\ x^2+5x-66=0 \end{gathered}`

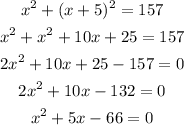
We now have a quadratic equation.

We can solve it as:

`\begin{gathered} x=(-5\pm√(5^2-4(1)(-66)))/(2(1)) \\ x=(-5\pm√(25+264))/(2) \\ x=(-5\pm√(289))/(2) \\ x=(-5\pm17)/(2) \\ \Rightarrow x_1=(-5-17)/(2)=(-22)/(2)=-11 \\ \Rightarrow x_2=(-5+17)/(2)=(12)/(2)=6 \end{gathered}`

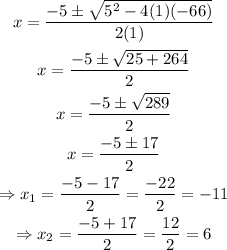
We have two possible solutions: -11 and 6.

We can check both:

1) If x = -11, then y is -6, and the sum of the squares is 121 + 36 = 157, so it is valid.

2) If x = 6, then y is 11 and the sum of the squares will also be 157, so it is also a valid solution.

Answer:

If both numbers are positive, they are 6 and 11.

If negative numbers are allowed, the pair of numbers -11 and -6 is a valid solution too.