Question

Given the following hypotheses:H0: u = 590H1: u ≠ 590A random sample of 15 observations is selected from a normal population. The sample mean was 595 and the sample standarddeviation 8. Using the 0.05 significance level:a. State the decision rule. Reject H0 when the teststatistic is outside the interval ( , )

Answer 1

Here, we are give the following:

Sample mean, x' = 595

Sample size, n = 15

Significance level = 0.05

Null and alternative hyporthesis:

H0: u = 590

H1: u ≠ 590

a) The decision rule:

The decision rule here, will be to reject the null hypothesis, H0, when the test statistic is outside the interval

Here, degrees of freedom, df = 15 -1 = 14

Therefore,

The critical values for t will be:

`( t_0._0_2_5_/_2, _1_4, t_1 -_0._0_2_5_/_2, _1_4,)`

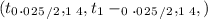
Using the crtical value value table, we have:

at significance level of 0.025 and df = 14, t = -2.1448

at = 1 - 0.025 = 0.975, and df = 14, t = 2.1448

We can now say that:

The decision rule here, will be to reject the null hypothesis, H0, when the test statistic is outside the interval(-2.1448, 2.1448)

This means we are to reject H0 if t is greater than 2.1448 or when t is less than -2.1448