Question

I need help on the first one it’s confusing for me and it’s geometry

Answer 1

$ 6'282,312.524

Step-by-step explanation

Step 1

find the length of the street:

we have a rigth triangle, then

Let

`\begin{gathered} \text{side}1=\text{ 6 miles} \\ \text{side}2=\text{ 9 miles} \\ \text{hypotenuse = new str}et=\text{ h} \end{gathered}`

so, we need to find the valur for hypotenuse, to do that, we can use the Pythagorean theorem, it states that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse (the side opposite the right angle)

so

`\begin{gathered} (Side1)^2+(Side2)^2=h^2 \\ \text{replace} \\ (6m)^2+(9m)^2=h^2 \\ 36m^2+81m^2=h^2 \\ 117m^2=h^2 \\ \sqrt[]{117m^2}=√(h^2) \\ \text{hence} \\ h=10.81\text{ mi} \end{gathered}`

Step 2

find the total cost,

a) convert the length from miles to ft,so

`\begin{gathered} 10.81\text{ mi(}\frac{5280\text{ ft}}{1\text{ mi}}\text{)}=5711.9322 \\ 5711.9322\text{ft} \end{gathered}`

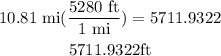
b) finally, to know the total cost multiply the length by the rate,so

`\begin{gathered} \text{total cost= ralte}\cdot length\text{ ( ft)} \\ \text{total cost= }110\frac{\text{ \$}}{ft}\cdot5711.9322\text{ ft} \\ \text{total cost= \$ }6^(\prime)282,321.542 \end{gathered}`

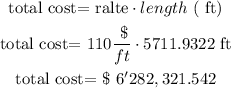
therefore, the estimated cost is

$ 6'282,312.524

I hope this helps you