Question

I’m really sick on this promise and i really need help

Answer 1

Analysis: We have an initial inequation; we need to isolate x in order to graph the solution.

`-4.4\ge1.6x-3.6`

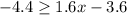
Let's add 3.6 on both sides:

`\begin{gathered} -4.4+3.6\geqslant1.6x-3.6+3.6 \\ -0.8\ge1.6x \end{gathered}`

Now, let's divide by 1.6 into both sides to isolate x.

`\begin{gathered} (-0.8)/(1.6)\ge(1.6x)/(1.6) \\ -0.5\ge x \\ x\leq-0.5 \end{gathered}`

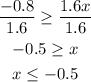
After we simplify the inequation until x is less or equal to -0.5, now we can graph the solution.

X has to be equal to or less than -0.5. That graph corresponds to the first option.