Question

A person invests 4000 dollars in a bank. The bank pays 5.75% interest compounded quarterly. To the nearest tenth of a year, how long must the person leave the money in the bank until it reaches 5900 dollars?

Answer 1

Given:

A person invests 4000 dollars in a bank.

so, the initial balance = P = 4000

The interest rate = r = 5.75% = 0.0575

Compounded quarterly, n = 4

We will find the time (t) to reach 5900

We will use the following formula:

`A=P(1+(r)/(n))^(nt)`

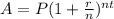
Substitute with the given values then solve for (t)

`\begin{gathered} 5900=4000(1+(0.0575)/(4))^(4t) \\ (5900)/(4000)=1.014375^(4t) \\ \end{gathered}`

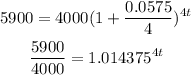
Taking the natural logarithm for both sides:

`\begin{gathered} \ln (5900)/(4000)=4t\cdot\ln 1.014375 \\ \\ t=(\ln (5900)/(4000))/(4\ln 1.014375)\approx6.8077 \end{gathered}`

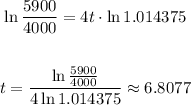
Rounding to the nearest tenth of a year

So, the answer will be t = 6.8 years