The volume of a prism is equal to the area A of its base times its height h:
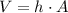
On the other hand, there is a formula to find the area of a triangle if the lengths of 3 sides are given.
Let a, b and c be the lengths of the sides of a triangle.
We define the semiperimeter s of the triangle as:
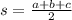
Then, the area of the triangle is given by the Heron's formula:
![A=\sqrt[]{s(s-a)(s-b)(s-c)}](https://img.qammunity.org/2023/formulas/mathematics/college/t3rmhsk71nltcmgtu237bvtgrmrx89v4xv.png)
Replace a=3cm, b=6cm and c=5cm to find s:
![s=\frac{3\operatorname{cm}+6\operatorname{cm}+5\operatorname{cm}}{2}=\frac{14\operatorname{cm}}{2}=7\operatorname{cm}]()
Replace the values of a, b and c as well as s=7cm into Heron's formula to find the area of the triangular base:
![\begin{gathered} A=\sqrt[]{7\operatorname{cm}\cdot(7cm-3cm)(7cm-6cm)(7cm-5cm)} \\ =\sqrt[]{7\operatorname{cm}\cdot4\operatorname{cm}\cdot1\operatorname{cm}\cdot2\operatorname{cm}} \\ =\sqrt[]{56\operatorname{cm}^4} \\ =\sqrt[]{56}\cdot cm^2 \\ \approx7.48\operatorname{cm}^2 \end{gathered}]()
Replace the value of A and h=15cm into the equation to find the volume of the prism:
![\begin{gathered} V=h\cdot A \\ =15\operatorname{cm}\cdot\sqrt[]{56}\cdot cm^2 \\ =15\cdot\sqrt[]{56}\cdot cm^3 \\ \approx112.25\operatorname{cm}^3 \end{gathered}]()
Therefore, to the nearest cubic centimeter, the volume of the prism is 112 cm^3.