Question

A certain game consists of rolling a single fair die and pays off as follows: $9 for a 6, $3 for a 5, $1 for a 4, and no payoff otherwise. Find the expected winnings for this game.

Answer 1

In this case, we'll have to carry out several steps to find the solution.

Step 01:

Data:

Die:

$9 ===> 6

$3 ===> 5

$1 ===> 4

expected winnings = ?

Step 02:

Expected winnings

probability (6) = favorable outcomes / total outcomes

= 1/6

probability (5) = 1/6

probability (4) = 1/6

`E\text{ (die winnings) = \$9}\cdot(1)/(6)+\text{ \$3 }\cdot(1)/(6)\text{ + \$1 }\cdot\text{ }(1)/(6)`

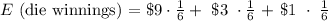
E (die winnings) = $13 / 6 = $2.17

The answer is:

The expected winnings are $2.17