Question

Right triangle XYZ hasm∠Y = 90° , m∠X = 45° and side XZ = 36Find the area of triangle XYZ.

Answer 1

Given:

In a right triangle XYZ,

`\begin{gathered} m\angle Y=90\degree \\ m\angle X=45\degree \\ \text{The side, }XZ=36 \end{gathered}`

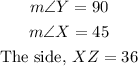
To find the area of the triangle:

Let us find the base and height of the triangle.

Using the trigonometric ratio,

`\begin{gathered} \sin \theta=(Opp)/(Hyp) \\ \sin 45^(\circ)=(YZ)/(XZ) \\ \frac{1}{\sqrt[]{2}}=(YZ)/(36) \\ YZ=\frac{36}{\sqrt[]{2}} \\ =\frac{36}{\sqrt[]{2}}*\frac{\sqrt[]{2}}{\sqrt[]{2}} \\ =\frac{36\sqrt[]{2}}{2} \\ YZ=18\sqrt[]{2}\ldots\ldots\ldots(1) \end{gathered}`

Using the trigonometric ratio,

`\begin{gathered} \cos \theta=\frac{\text{Adj}}{Hyp} \\ \cos 45^(\circ)=(XY)/(XZ) \\ \frac{1}{\sqrt[]{2}}=(XY)/(36) \\ XY=\frac{36}{\sqrt[]{2}} \\ =\frac{36}{\sqrt[]{2}}*\frac{\sqrt[]{2}}{\sqrt[]{2}} \\ =\frac{36\sqrt[]{2}}{2} \\ XY=18\sqrt[]{2}\ldots\ldots\ldots(2) \end{gathered}`

The formula of area of the triangle is,

`\begin{gathered} A=(1)/(2)* base* height \\ =(1)/(2)* XY* YZ \\ =(1)/(2)*18\sqrt[]{2}*18\sqrt[]{2} \\ =324 \end{gathered}`

Hence, the area of the triangle is 324 square units.