Question

34 mL of nitrogen gas is measured at 21.0 Celsius and .953 ATM pressure calculate the volume at STP

Answer 1

To solve this question, we would use the combined gas equation which comprises of Boyle's law, Charles law and pressure law.

The equation is given as

`\begin{gathered} v_1=34mL \\ T_1=21^0C=21+273.15=294.15K \\ P_1=0.953\text{atm} \end{gathered}`

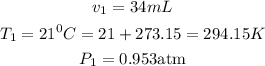
At STP (standard temperature and pressure), the temperature and pressure changes to

`\begin{gathered} p_2=1\text{atm} \\ t_2=273.15K_{} \end{gathered}`

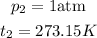
Now, combining the data above, we can find the change in volume (v₂)

`\begin{gathered} (p_1v_1)/(t_1)=(p_2v_2)/(t_2) \\ v_2=(p_1v_1t_2)/(p_2t_1) \\ \end{gathered}`

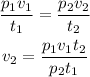
Let's substitute the values into the equation above and solve for v₂

`\begin{gathered} v_2=(p_1v_1t_2)/(p_2t_1) \\ v_2=(0.953*34*273.15)/(1*294.15) \\ v_2=30.1mL \end{gathered}`

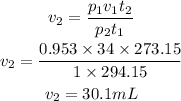
From the calculations above, the volume at STP is 30.1mL