Question

The current (I) in a wire varies directly as the voltage (v) and inversely as the resistance (r). If the current is 27.5 amps when the voltage is 110 volts and the resistance is 4 ohms, find the current when the voltage is 125 volts and the resistance is 16 ohms. (Round your answer to two decimal places.)

Answer 1

Current (l) = 7.81 amps (rounded to 2 decimal places)

Step-by-step explanation

Declaration of Variables

Let l represent the current in a wire,

v represent the voltage, and

r represent the resistance

Desired Outcome

The current (l)

Equation formation

`\begin{gathered} l\propto(v)/(r) \\ l\text{ = }(kv)/(r) \end{gathered}`

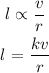
where k is the constant of proportionality.

Determine the value of k given l = 27.5, v = 110, and r = 4.

`\begin{gathered} l\text{ = }(kv)/(r) \\ 27.5\text{ = }(k*110)/(4) \\ 110k\text{ = 27.5}*4 \\ 110k\text{ = 110} \\ k\text{ = }(110)/(110) \\ k\text{ = 1} \end{gathered}`

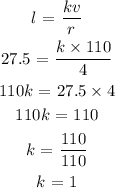
Find the current (l) given v = 125, and r = 16.

`\begin{gathered} l\text{ = }(kv)/(r) \\ l\text{ = }(1*125)/(16) \\ l\text{ = 7.8125 amps} \end{gathered}`

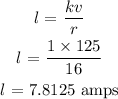
Hence, the current (l) when the voltage is 125 volts and the resistance is 16 ohms is 7.81 amps (rounded to 2 decimal places).