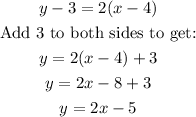point-slopeWe are required to get the equation of the line in the point-slope and slope-intercept forms.
A line given in the form: y = mx + b is given in the slope-intercept form where m and b are the slope and intercept on the vertical axis respectively.
A pair of parallel lines have the same gradient and we will leverage this fact to get the equation of the line that passes through the point (4,3).
The point-slope slope form of a line is:
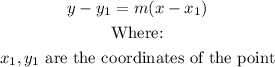
We therefore have:
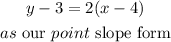
Converting to slope-intercept form: