Given:
(a) Circumference of a circle is
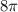
To find: Area of circle
Circumference of circle is given as:
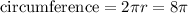
where, r is radius of circle
On solving,
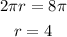
Area of circle is given by formula:
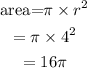
Hence, area of circle is :
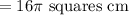
(b) Radius of circle is given 'r' and square of length is given 'b'
and they have equal areas.
To find: r in terms of b.
According to the question,
Area of circle= Area of square
![\begin{gathered} \pi* r^2=b^2 \\ r^2=(b^2)/(\pi) \\ r=\sqrt[]{(b^2)/(\pi)} \\ =\frac{b}{\sqrt[]{\pi}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/4dnuyeelmqhk77e2bzrxb1ndpq9lfhibds.png)
Hence,
![r=\frac{b}{\sqrt[]{\pi}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/dn7paix0lzkoqav6d6sr4m5hyvkvacc49a.png)