Question

a. if a circle has a circumference of 8π cm, what is it's area? b. If a circle of radius r, and a square with a side length b have equal areas, express r in terms of b.

Answer 1

Given:

(a) Circumference of a circle is

`8\pi`

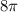
To find: Area of circle

Circumference of circle is given as:

`\text{circumference}=2\pi r=8\pi`

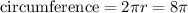
where, r is radius of circle

On solving,

`\begin{gathered} 2\pi r=8\pi \\ r=4 \end{gathered}`

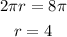
Area of circle is given by formula:

`\begin{gathered} \text{area=}\pi* r^2^{} \\ =\pi*4^2 \\ =16\pi \end{gathered}`

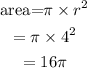
Hence, area of circle is :

`=16\pi\text{ squares cm}`

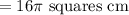
(b) Radius of circle is given 'r' and square of length is given 'b'

and they have equal areas.

To find: r in terms of b.

According to the question,

Area of circle= Area of square

`\begin{gathered} \pi* r^2=b^2 \\ r^2=(b^2)/(\pi) \\ r=\sqrt[]{(b^2)/(\pi)} \\ =\frac{b}{\sqrt[]{\pi}} \end{gathered}`

Hence,

`r=\frac{b}{\sqrt[]{\pi}}`