Question

The population mean annual salary for environmental compliance specialists is about $64,000. A random sample of 30 specialists is drawn from this population. Whatis the probability that the mean salary of the sample is less than $61,500? Assume o =$5,900.The probability that the mean salary of the sample is less than $61,500 is ____(Round to four decimal places as needed.)Interpret the results. Choose the correct answer below.A. Only 1.01% of samples of 30 specialists will have a mean salary less than $61,500. This is an unusual event. B. About 10.1% of samples of 30 specialists will have a mean salary less than $61,500. This is not an unusual eventC. Only 10.1% of samples of 30 specialists will have a mean salary less than $61,500. This is an unusual eventD About 1.01% of samples of 30 specialists will have a mean salary less than $61,500. This is not an unusual event

Answer 1

A. Only 1.01% of samples of 30 specialists will have a mean salary less than $61,500. This is an unusual event.

Step-by-step explanation:

• Population Mean = 64,000

,

• Sample = 30

,

• Raw Score = 61,500

,

• Standard Deviation = 5,900

First, we find the z-score using the formula below:

`z=\frac{x-\mu}{\frac{\sigma}{\sqrt[]{n}}}`

Substitute the given values:

`\begin{gathered} z=\frac{61500-64000}{5900/\sqrt[]{30}} \\ z=-2.32 \end{gathered}`

Next, from a z-score table:

`\begin{gathered} P(z<-2.32)=0.0102 \\ \approx1.01\% \end{gathered}`

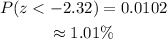
Therefore, the probability that the mean salary of the sample is less than $61,500 is 0.0102.

Next, we interpret the result.

• As a general rule, z-scores lower than -1.96 or higher than 1.96 are considered unusual. Since -2.32 is lower than -1.96, it is unusual.

Only 1.01% of samples of 30 specialists will have a mean salary less than $61,500. This is an unusual event.