Question

A child's toy soap bubble wand creates approximately spherical bubbles. The surface area of a soap bubble varies directly as the square of the radius of the bubble. If a bubble with a radius of 3 inches has a surface area of 113 square inches, what is the surface area (in square inches) of a bubble that has a radius of 4 inches? Round to the nearest tenth of a square inch. (See Example 2 in this section.)_______ in2

Answer 1

Given:

The surface area of a soap bubble varies directly as the square of the radius of the bubble.

Let the surface area = A

Let the radius = r

so,

`\begin{gathered} A\propto r^2 \\ A=k\cdot r^2 \end{gathered}`

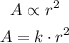
where: (k) is the constant of proportionality

If a bubble with a radius of 3 inches has a surface area of 113 square inches

so,

When r = 3 inches, A = 113 square inches

Substitute with (r) and (A) to find the value of (k)

`\begin{gathered} 113=k\cdot3^2 \\ 113=9k \\ k=(113)/(9) \end{gathered}`

so, the equation will be:

`A=((113)/(9))r^2`

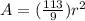
we will find the surface area when the radius = 4 inches

So, when r = 4 inches

`A=((113)/(9))\cdot4^2=(113)/(9)\cdot16=200.8889`

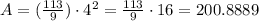
Rounding to the nearest tenth

So, the answer will be: the surface area = 200.9 square inches