Question

Mrs. Gomes found that 40% of students at her high school take chemistry. She randomly surveys 12 students. What is the probability that at most 4 students have taken chemistry? Round the answer to the nearest thousandth.READ ANSWERS!0.0080.4380.5620.665

Answer 1

If we don't allow to repeat a pick on the sample, than each student we pick will change the probability of picking the next one and, since we don't know the total number of students at her high school, we wouldn't be able to calculate this probability.

Thus, to calculate this with the provided information, we need to assume that we can repeat a student in the sample, that way the probability of picking a chemistry student will always be 40%.

So, with that assumption, we can use binomial probability to calculate the probability of picking at most from from that have taken chemistry on the 12 picked students.

Since we want at most 4, we have the consider the term of the binomial for which 0 students from chemistry were picked, the term for 1 from chesmitry, the term for 2, the term for 3 and the term for 4.

Let p be the probability of picking 1 student from chemistry, n be the total number of students picked and k be the number of students on those that are from chemistry. Then, each term will have the following:

`B(k)=(n!)/(k!(n-k)!)p^k(1-p)^(n-k)_{}`

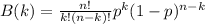
In this case, n is always 12 and p is always 0.4, so 1 - p is always 0.6.

k will vary from 0 to 4 and the total probability will be the sum of each term.

The term for 0 students from chemistry has k = 0, so:

`B(0)=(12!)/(0!(12-0)!)(0.4)^0(0.6)^(12-0)=1\cdot1\cdot(0.6)^(12)=0.0021767\ldots`

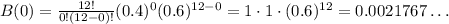
The term for 1 student from chemistry has k = 1, so:

`B(1)=(12!)/(1!(12-1)!)(0.4)^1(0.6)^(12-1)=12\cdot0.4\cdot(0.6)^(11)=0.0174142\ldots`

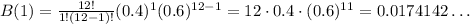
The term for 2 student from chemistry has k = 2, so:

`B(2)=(12!)/(2!(12-2)!)(0.4)^2(0.6)^(12-2)=(12\cdot11)/(2)\cdot(0.4)^2\cdot(0.6)^(10)=0.0638522\ldots`

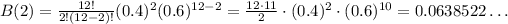
The term for 3 student from chemistry has k = 3, so:

`B(3)=(12!)/(3!(12-3)!)(0.4)^3(0.6)^(12-3)=(12\cdot11\cdot10)/(3\cdot2)\cdot(0.4)^3\cdot(0.6)^9=0.1418939\ldots`

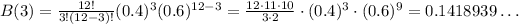
The term for 4 student from chemistry has k = 4, so:

`B(4)=(12!)/(4!(12-4)!)(0.4)^4(0.6)^(12-4)=(12\cdot11\cdot10\cdot9)/(4\cdot3\cdot2)\cdot(0.4)^4\cdot(0.6)^8=0.2128409\ldots`

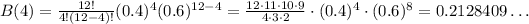
So, the total probability will be the sum of all these term:

`\begin{gathered} P=B(0)+B(1)+B(2)+B(3)+B(4) \\ P=0.0021767\ldots+0.0174142\ldots+0.0638522\ldots+0.1418939\ldots+0.2128409\ldots \\ P=0.4381782\ldots\approx0.438 \end{gathered}`

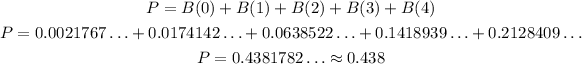
So, the probability is approximately 0.438.