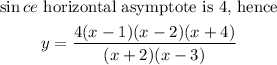Rational functions are functions that have a numerator part and a denominator part.
Vertical asymptotes means that the function is undefined at the given point, since
the function is undefined when the denominator is zero. In this case, the denominator
part of the function becomes
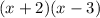
x-intercepts means that if we set the numerator part equal to zero, the function becomes zero.
In this case, the numerator part of the function becomes