Question

What is the current through each resistor in the parallel portion?

Answer 1

Given:

Two resistors each of resistance R = 60 ohms are connected in parallel.

A resistance R' = 30 ohms is connected in series with the parallel combination.

The voltage across the circuit is V = 120 V.

To find the current through each resistor in the parallel portion.

Step-by-step explanation:

The equivalent resistance of the resistors connected in parallel will be

`\begin{gathered} (1)/(R_p)=(1)/(R)+(1)/(R) \\ =(1)/(60)+(1)/(60) \\ R_p=\text{ }(60)/(2) \\ =30\text{ }\Omega \end{gathered}`

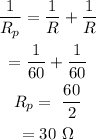
In a series combination, the voltage will be the sum of voltages across each resistor while the current remains the same.

In parallel combination, the voltage remains the same while the current is the sum of currents through each resistor.

Voltage in series combination will be

`\begin{gathered} V=V_(Rp)+V^(\prime) \\ V=V_(30)+V_(30) \\ V_(30)=\text{ }(V)/(2) \\ =(120)/(2) \\ =60\text{ V} \end{gathered}`

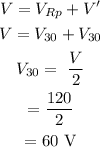
The voltage across each resistor in the parallel combination will be 60 ohms.

The current in the series combination will be the same.

According to the Ohm's law, the current will be

`\begin{gathered} V^(\prime)=I^(\prime)R^(\prime) \\ I^(\prime)=(V^(\prime))/(R^(\prime)) \\ =(60)/(30) \\ =2\text{ A} \end{gathered}`

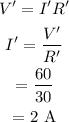
The current in the parallel combination will be the sum of individual current

`I^(\prime)=I_1+I_2`

Since the voltage across the parallel combination is the same and the resistance is also the same, so

`\begin{gathered} I_1=I_2 \\ =I_p \end{gathered}`

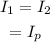
Thus, the current through each resistor in parallel combination will be

`\begin{gathered} I^(\prime)=I_p+I_p \\ I_p=(I^(\prime))/(2) \\ =(2)/(2) \\ =\text{ 1 A} \end{gathered}`

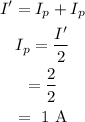
Hence, the current through each resistor in the parallel portion is 1 A